This article is about image binarization using the Otsu method. A simple C++ implementation of the Otsu thresholding algorithm based on the CImg library is shown. In Part 1 of my “Night sky image processing” series I have taken a look on anisotropic diffusion in order to reduce the image noise.
Introduction to Thresholding
The next topic I want to have a look at is thresholding. In this step the algorithm decides which pixels belong to the background and which pixels belong to a star. However, before the algorithm can decide which pixels belong to a particular star (also called clustering – see part 3) it first has to generally decide which pixels belongs to any star and which pixels belong to the background. This process is called thresholding i.e. converting a grey-scale image into a binary image. There are many different thresholding algorithms out there. All have there advantages and drawbacks. I found ImageJ very helpful to test different thresholding algorithms.
Why Otsu Thresholding for astro images
After trying different ones I found that Otsu’s method does a quite good job. After further reading I found out that this method is especially useful for images with bi-modal histograms. To my knowledge night shy images usually do not have bi-modal histograms. However, so far Otsu’s method still gave very good results with my star images. Furthermore it is relatively efficient and simple to implement. For those reasons I decided to go this way.
Introduction to Otsu Thresholding
Otsu’s algorithm tries to find the threshold so that the variance of all pixel values in the foreground and the variance of all pixel values in the background becomes minimal. The variance is a measure of the spread. The smaller the variance of for example the foreground pixel values, the closer the gray levels of the pixels and the more likely it is that they belong together. At least that’s how I understand Otsu’s method.
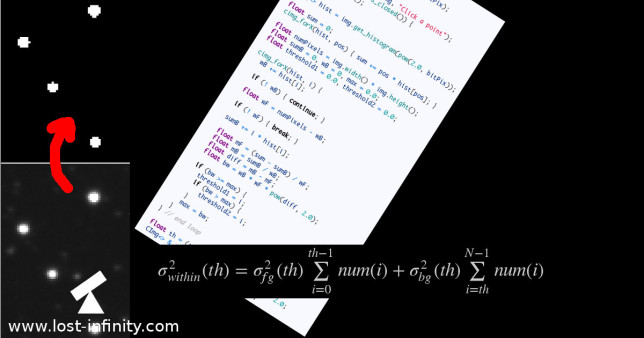
The following formula calculates a kind of “mean” variance $\sigma^2_{within}(th)$ of the foreground variance $\sigma^2_{fg}(th)$ and the background variance $\sigma^2_{bg}(th)$. In fact it is no mean but a weighted sum of both. The weights are the number of pixels in the respective group:
$$\sigma^2_{within}(th)=\sigma^2_{fg}(th) \sum\limits_{i=0}^{th-1} {num(i)} + \sigma^2_{bg}(th) \sum\limits_{i=th}^{N-1} {num(i)}$$
Continue reading →