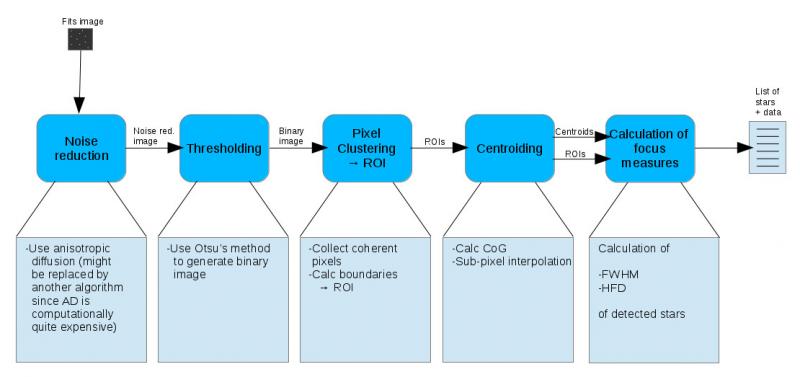
Calculation of a SNR for stars
This article shows how to calculate the 2D signal-to-noise ratio (SNR). Furthermore, it demonstrates how the $SNR$ can be used to decide if there is a potential star in the image.
Long story short – I was looking for a way to detect more or less reliably if a user selected a region which contains a star. I wanted to be able to clearly distinguish between the following two images:
Solution with the CImg library
After a long journey I finally ended up with the following solution. It is based on the CImg library which in a way calculates the Signal-to-noise ratio (SNR):
CImg <uint16_t> image; ... double q = image.variance(0) / image.variance_noise(0); double qClip = (q > 1 ? q : 1); double snr = std::sqrt(qClip - 1);
For the two images above the code gives the following results:
~/snr$ ./snr no_star.fits SNR: 0.0622817 ~snr$ ./snr test_star.fits SNR: 1.5373
For many people this is where the journey ends. But for some of you it may just begin :). Follow me into the rabbit hole and find out why the solution shown above actually works…
Continue reading →