In Part 4 of my “Night sky image processing” Series I wrote about star centroid determination with sub-pixel accuracy. Based on this centroid position the FWHM determination of the star takes place. The FWHM (Full Width Half Maximum) value is a measurement for the star width. In this part I write about the so called curve-fitting which is helpful to determine the FWHM value from such an image. Note that for the following calculation and implementation I do not consider the sub-pixel determination of the centroid.
Determination of the FWHM
Let’s say we want to determine the FWHM in x-direction (red line). There is of course also one in y-direction. Basically, what happens is:
- Extract the pixel line through the centroid in x direction (those gray-level values usually form a Gaussian distribution: $$y(t)|_{b, p, c, w} = b + p \cdot e^{-\frac{1}{2} \cdot \big(\frac{t – c}{w}\big)^2}$$ We define a “data-point” as (x,y)=(pixel x-position, pixel gray-level value).
- Based on those (x,y) data-points determine the 4 parameters of a Gaussian curve so that the Gaussian curve and the data-points fit “as good as possible”. As fitting algorithm we use the so called “Levenberg-Marquart” algorithm. It tries to minimize the quadratic error between the data-points and the curve.
- The result is a Gaussian curve i.e. a parameter set which describes the curve (c=center, p=peak, b=base and the w=mean width). One of those parameters – the mean width is the FWHM value.
A C++ implementation

NOTE: All the source codes of this “Night sky image processing” series presented in part 1-7 are also available on github in the star_recognizer repository.
The C++ implementation below uses the GSL (GNU scientific library) to make use of the Levenberg-Marquart algorithm. The primary application of the Levenberg–Marquardt algorithm is the least squares curve fitting problem. Imagine you have a set of data points and you want to determine all parameters of a certain curve so that the curve fits all the data points as “good as possible”. Usually one has an idea of how the data looks like. It could be a parable or a Gaussian curve or something else. As already mentioned in this case it is a Gaussian curve. The math behind Levenberg-Marquart is very well explained on Wikipedia. Basically one just has to calculate some derivatives of the curve one wants to fit.
The implementation below makes use of the C++ Traits mechanism. The idea is to supply the curve details (derivations, parameters, …) as template parameters to the CurveFitTmplT template. I made this design decision since the curve type (e.g. a Gaussian curve) usually can be made already at compile-time. One more thing to mention might be the “DataAccessor” of the fitGslLevenbergMarquart template function. The API user can choose the form of his/her input data without modifying the template source and without copying the data to another internal data structure.
#include <iostream>
#include <array>
#include <vector>
#include <list>
#include <gsl/gsl_multifit_nlin.h>
using namespace std;
/**********************************************************************
* Helper classes
**********************************************************************/
struct DataPointT {
float x;
float y;
DataPointT(float inX = 0, float inY = 0) : x(inX), y(inY) {}
};
typedef vector<DataPointT> DataPointsT;
struct GslMultiFitDataT {
float y;
float sigma;
DataPointT pt;
};
typedef vector<GslMultiFitDataT> GslMultiFitParmsT;
/**********************************************************************
* Curve to fit to is supplied by traits.
**********************************************************************/
template <class FitTraitsT>
class CurveFitTmplT {
public:
typedef typename FitTraitsT::CurveParamsT CurveParamsT;
/**
* DataAccessor allows specifying how x,y data is accessed.
* See https://en.wikipedia.org/wiki/Approximation_error for expl. of rel and abs errors.
*/
template<typename DataAccessorT> static int
fitGslLevenbergMarquart(const typename DataAccessorT::TypeT & inData, typename CurveParamsT::TypeT * outResults,
double inEpsAbs, double inEpsRel, size_t inNumMaxIter = 500) {
GslMultiFitParmsT gslMultiFitParms(inData.size());
// Fill in the parameters
for (typename DataAccessorT::TypeT::const_iterator it = inData.begin(); it != inData.end(); ++it) {
size_t idx = std::distance(inData.begin(), it);
const DataPointT & dataPoint = DataAccessorT::getDataPoint(idx, it);
gslMultiFitParms[idx].y = dataPoint.y;
gslMultiFitParms[idx].sigma = 0.1f;
gslMultiFitParms[idx].pt = dataPoint;
}
// Fill in function info
gsl_multifit_function_fdf f;
f.f = FitTraitsT::gslFx;
f.df = FitTraitsT::gslDfx;
f.fdf = FitTraitsT::gslFdfx;
f.n = inData.size();
f.p = FitTraitsT::CurveParamsT::_Count;
f.params = & gslMultiFitParms;
gsl_vector * guess = gsl_vector_alloc(FitTraitsT::CurveParamsT::_Count); // Allocate the guess vector
FitTraitsT::makeGuess(gslMultiFitParms, guess); // Make initial guesses based on the data
// Create a Levenberg-Marquardt solver with n data points and m parameters
gsl_multifit_fdfsolver * solver = gsl_multifit_fdfsolver_alloc(gsl_multifit_fdfsolver_lmsder,
inData.size(), FitTraitsT::CurveParamsT::_Count);
gsl_multifit_fdfsolver_set(solver, & f, guess); // Initialize the solver
int status, i = 0;
// Iterate to to find a result
do {
i++;
status = gsl_multifit_fdfsolver_iterate(solver); // returns 0 in case of success
if (status) { break; }
status = gsl_multifit_test_delta(solver->dx, solver->x, inEpsAbs, inEpsRel);
} while (status == GSL_CONTINUE && i < inNumMaxIter);
// Store the results to be returned to the user (copy from gsl_vector to result structure)
for (size_t i = 0; i < FitTraitsT::CurveParamsT::_Count; ++i) {
typename FitTraitsT::CurveParamsT::TypeE idx = static_cast<typename FitTraitsT::CurveParamsT::TypeE>(i);
(*outResults)[idx] = gsl_vector_get(solver->x, idx);
}
// Free GSL memory
gsl_multifit_fdfsolver_free(solver);
gsl_vector_free(guess);
return status;
}
};
/**********************************************************************
* Gaussian fit traits
**********************************************************************/
class GaussianFitTraitsT {
private:
public:
struct CurveParamsT {
// b = base, p = peak, c = center in x, w = mean width (FWHM)
enum TypeE { B_IDX = 0, P_IDX, C_IDX, W_IDX, _Count };
struct TypeT : public std::array<float, TypeE::_Count> {
TypeT(const gsl_vector * inVec = 0) {
for (size_t i = 0; i < TypeE::_Count; ++i) {
TypeE idx = static_cast<TypeE>(i);
(*this)[i] = (inVec ? gsl_vector_get(inVec, idx) : 0);
}
}
};
};
/* Makes a guess for b, p, c and w based on the supplied data */
static void makeGuess(const GslMultiFitParmsT & inData, gsl_vector * guess) {
size_t numDataPoints = inData.size();
float y_mean = 0;
float y_max = inData.at(0).pt.y;
float c = inData.at(0).pt.x;
for(size_t i = 0; i < numDataPoints; ++i) {
const DataPointT & dataPoint = inData.at(i).pt;
y_mean += dataPoint.y;
if(y_max < dataPoint.y) {
y_max = dataPoint.y;
c = dataPoint.x;
}
}
y_mean /= (float) numDataPoints;
float w = (inData.at(numDataPoints - 1).pt.x - inData.at(0).pt.x) / 10.0;
gsl_vector_set(guess, CurveParamsT::B_IDX, y_mean);
gsl_vector_set(guess, CurveParamsT::P_IDX, y_max);
gsl_vector_set(guess, CurveParamsT::C_IDX, c);
gsl_vector_set(guess, CurveParamsT::W_IDX, w);
}
/* y = b + p * exp(-0.5f * ((t - c) / w) * ((t - c) / w)) */
static float fx(float x, const CurveParamsT::TypeT & inParms) {
float b = inParms[CurveParamsT::B_IDX];
float p = inParms[CurveParamsT::P_IDX];
float c = inParms[CurveParamsT::C_IDX];
float w = inParms[CurveParamsT::W_IDX];
float t = ((x - c) / w);
t *= t;
return (b + p * exp(-0.5f * t));
}
/* Calculates f(x) = b + p * e^[0.5*((x-c)/w)] for each data point. */
static int gslFx(const gsl_vector * x, void * inGslParams, gsl_vector * outResultVec) {
CurveParamsT::TypeT curveParams(x); // Store the current coefficient values
const GslMultiFitParmsT * gslParams = ((GslMultiFitParmsT*) inGslParams); // Store parameter values
//Execute Levenberg-Marquart on f(x)
for(size_t i = 0; i < gslParams->size(); ++i) {
const GslMultiFitDataT & gslData = gslParams->at(i);
float yi = GaussianFitTraitsT::fx((float) gslData.pt.x, curveParams);
gsl_vector_set(outResultVec, i, (yi - gslData.y) / gslData.sigma);
}
return GSL_SUCCESS;
}
/* Calculates the Jacobian (derivative) matrix of f(x) = b + p * e^[0.5*((x-c)/w)^2] for each data point */
static int gslDfx(const gsl_vector * x, void * params, gsl_matrix * J) {
// Store parameter values
const GslMultiFitParmsT * gslParams = ((GslMultiFitParmsT*) params);
// Store current coefficients
float p = gsl_vector_get(x, CurveParamsT::P_IDX);
float c = gsl_vector_get(x, CurveParamsT::C_IDX);
float w = gsl_vector_get(x, CurveParamsT::W_IDX);
// Store non-changing calculations
float w2 = w * w;
float w3 = w2 * w;
for(size_t i = 0; i < gslParams->size(); ++i) {
const GslMultiFitDataT & gslData = gslParams->at(i);
float x_minus_c = (gslData.pt.x - c);
float e = exp(-0.5f * (x_minus_c / w) * (x_minus_c / w));
gsl_matrix_set(J, i, CurveParamsT::B_IDX, 1 / gslData.sigma);
gsl_matrix_set(J, i, CurveParamsT::P_IDX, e / gslData.sigma);
gsl_matrix_set(J, i, CurveParamsT::C_IDX, (p * e * x_minus_c) / (gslData.sigma * w2));
gsl_matrix_set(J, i, CurveParamsT::W_IDX, (p * e * x_minus_c * x_minus_c) / (gslData.sigma * w3));
}
return GSL_SUCCESS;
}
/* Invokes f(x) and f'(x) */
static int gslFdfx(const gsl_vector * x, void * params, gsl_vector * f, gsl_matrix * J) {
gslFx(x, params, f);
gslDfx(x, params, J);
return GSL_SUCCESS;
}
};
/**********************************************************************
* Custom data structure + accessor
**********************************************************************/
typedef pair<float, float> MyDataPointT;
typedef list<MyDataPointT> MyDataContainerT;
class MyDataAccessorT {
public:
typedef MyDataContainerT TypeT;
static DataPointT getDataPoint(size_t inIdx, TypeT::const_iterator inIt) {
DataPointT dp(inIt->first /*inIdx*/, inIt->second /*y*/);
return dp;
}
};
/**********************************************************************
* Main
**********************************************************************/
int main(void) {
// Fill data container with some gauss shaped data
MyDataContainerT dataPointsToFit;
dataPointsToFit.push_back(make_pair(0, 21));
dataPointsToFit.push_back(make_pair(1, 26));
dataPointsToFit.push_back(make_pair(2, 46));
dataPointsToFit.push_back(make_pair(3, 87));
dataPointsToFit.push_back(make_pair(4, 129));
dataPointsToFit.push_back(make_pair(5, 123));
dataPointsToFit.push_back(make_pair(6, 72));
dataPointsToFit.push_back(make_pair(7, 36));
dataPointsToFit.push_back(make_pair(8, 24));
dataPointsToFit.push_back(make_pair(9, 21));
// Do the LM fit
typedef CurveFitTmplT<GaussianFitTraitsT> GaussMatcherT;
typedef GaussMatcherT::CurveParamsT CurveParamsT;
CurveParamsT::TypeT gaussCurveParms;
GaussMatcherT::fitGslLevenbergMarquart<MyDataAccessorT>(dataPointsToFit, & gaussCurveParms, 0.1f /*EpsAbs*/, 0.1f /*EpsRel*/);
// Print calculated curve parameters and data points (x,y) + y_fit value
cerr << "base = " << gaussCurveParms[CurveParamsT::B_IDX]
<< ", peak = "<< gaussCurveParms[CurveParamsT::P_IDX]
<< ", center = "<< gaussCurveParms[CurveParamsT::C_IDX]
<< ", mean width (fwhm) = "<< gaussCurveParms[CurveParamsT::W_IDX]
<< endl << endl;
// Print data values
cerr << "# Data values" << endl;
cerr << "# X Y" << endl;
for(MyDataContainerT::iterator it = dataPointsToFit.begin(); it != dataPointsToFit.end(); ++it) {
cerr << it->first << " " << it->second << endl;
}
cerr << endl;
// Print curve values
cerr << "# Curve values" << endl;
cerr << "# X Y" << endl;
for(float f = 0.0; f < dataPointsToFit.size(); f += 0.5) {
cerr << f << " " << GaussianFitTraitsT::fx(f, gaussCurveParms) << endl;
}
return 0;
}
The code above can be compiled using the following command:
g++ -std=c++0x curve_fitting.C -lgsl -lgslcblas -o gauss_curve_fit
The output of the upper program is as follows:
$ ./gauss_curve_fit base = 21.1184, peak = 112.746, center = 4.35523, mean width (fwhm) = 1.3227 # Data values # X Y 0 21 1 26 2 46 3 87 4 129 5 123 6 72 7 36 8 24 9 21 # Curve values # X Y 0 21.6171 0.5 22.7304 1 25.6353 1.5 32.0896 2 44.2182 2.5 63.2787 3 87.8205 3.5 112.597 4 129.87 4.5 133.191 5 121.234 5.5 98.6437 6 73.1573 6.5 51.3983 7 36.3913 7.5 27.7961 8 23.6493 8.5 21.9499 9 21.3552 9.5 21.1768
The data points can be directly copy/pasted to a file and then loaded into gnuplot. The file are available for download here and here.
$ gnuplot gnuplot> plot "data_curve.dat" with line, "data_orig.dat" lt rgb "blue"
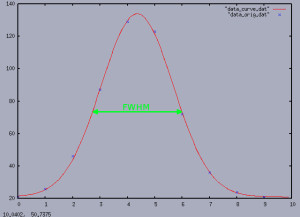
Result
The right picture shows the result of the gnuplot execution. The red line represents the “curve values”. The blue points show the data points to which the curve should match as good as possible. In this case the curve is pretty close to the actual data points. In addition the green line indicates the the actual FWHM value. Beside some other measurements the FWHM value is helpful to bring the camera into the focus. Hence, the code above can be helpful for a software which automatically tries to find the best focus position – i.e. trying to minimize the FWHM depending on the focus position.
In Part 6 of my “Night sky image processing” Series I am going to have a look at the calculation of the so called Half-Flux Diameter Value (HFD) which can also be very helpful to determine the best focus.
Last updated: June 9, 2022 at 23:43 pm





























If the star is saturated it becomes more difficult. There is a simpler method. I do it as follows:
1) Determine the background level by the averaging the boarders
2) Calculate the standard deviation of the background.
Signal is anything 5 times standard deviation above the background
3) Determine the maximum signal level of region of interest.
4) Count pixels which are equal or above half maximum level.
5) Use the pixel count as area and calculate the diameter of that area as diameter:=2 *sqrt(count/pi).
Pascal source available at HNS_FV fits viewer program.
Han.K
Hello Han.K, thanks for the info. Currently I am a little short on time but I will give it a try sooner or later. Best regards!