In Part 5 of my “Night sky image processing” Series I wrote about measuring the FWHM value of a star using curve fitting. Another measure for the star focus is the Half Flux Diameter (HFD). It was invented by Larry Weber and Steve Brady. The main two arguments for using the HFD is robustness and less computational effort compared to the FWHM approach.

There is another article about the HFD available here. Another short definition of the HFD I found here. The original paper from Larry Weber and Steve Bradley is available here.

Definition of the HFD?

Let’s start with the definition: “The HFD is defined as the diameter of a circle that is centered on the unfocused star image in which half of the total star flux is inside the circle and half is outside.”

In a mathematical fashion this looks like this:

$$\sum\limits_{i=0}^{N} V_i \cdot (d_i – HFR) = 0 \Leftrightarrow HFR = \frac{\sum\limits_{i=0}^{N} V_i \cdot d_i}{\sum\limits_{i=0}^{N} V_i}$$

where:

• $V_i$ is the pixel value minus the mean background value (!)
• $d_i$ is the distance from the centroid to each pixel
• $N$ is the number of pixels in the outer circle
• $HFR$ is the Half Flux Radius for which the sum becomes $0$

HFD and HFR

I decided to put the formula here because it makes it easier to explain what is going on. In contrast to the definition in the other article I decided to name $H$ Half Flux Radius ($HFR$) instead. This is because as far as I understand the formula $HFR$ is just the “mean radius” (and not the diameter) for which the sum becomes $0$. In fact all the “magic” is that the difference $d_i – HFR$ becomes negative for all the pixels which are inside the inner circle ($d_i < HFR$) and positive for all which are outside the inner circle ($d_i > HFR$). It is easy to calculate $HFR$ after transposing the equation.

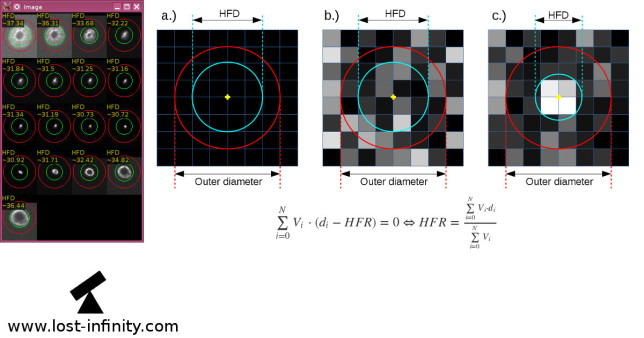
Subtracting the mean background

NOTE: It is important to subtract the mean background value from each pixel before calculating the HFD value. Otherwise – depending on how big the mean background value is – one might get quite interesting results. The right image shows the result if the mean background value is not subtracted. The calculated HFD value almost does not change for the different stars. The reason is quite simple: “Every little helps.” The flux of the many “black” pixels around adds up and has a significant effect on the calculation of the HFD. In fact there are just a few very bright pixels (lets say with ~16000 ADUs). In contrast there are > 2500 pixels with ~500 ADUs what in sum creates a much bigger flux than a few very bright pixels. The visual impression – the dark background in the star images – might lead into a wrong direction here. If the mean background is not subtracted, the result is shown in figure on the right.

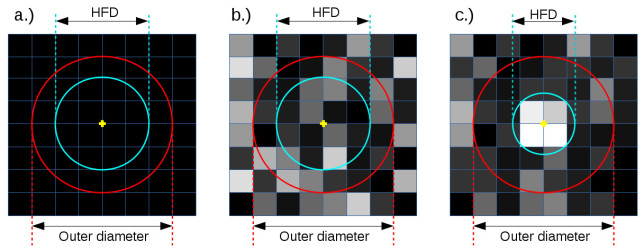
Understanding the HFD

In case a.) the flux is the same for each pixel (a more theoretical case of course). Then the two areas $A_{out}-A_{in}$ and $A_{in}$ would be equal and the HFD would be the diameter of the inner circle. This actually makes quite clear what the HFD means: The diameter of a circle which exactly cuts the total “flux” in the outer circle into half – i.e. half of the flux is inside the inner circle and half of the flux is in between the inner and the outer circle.

In this case the HFD would be $\sqrt{2} \cdot R_{out}$. The derivation is quite simple:

$$\begin{align}A_{out} &= \pi \cdot R_{out}^2 \\ A_{in} &= \pi \cdot R_{in}^2 \\ A_{in} &= \frac{A_{out}}{2} \\ \Rightarrow \frac{\pi \cdot R_{out}^2}{2} &= \pi \cdot R_{in}^2 \Leftrightarrow R_{in} = \sqrt{\frac{R_{out}^2}{2}} \\ \Rightarrow HFD &= 2 \cdot R_{in} \\ &= \sqrt{2} \cdot R_{out} \end{align}$$

One exception is the case when there is no flux at all (i.e. a totally black image). In that case the HFD actually does not exist since there would be a division by 0. However, for this implementation I decided to return a theoretical value of $\sqrt{2} \cdot R_{out}$ in this rather theoretical case.

In case b.) there is just noise but no star. The noise is more or less equally distributed and hence the $HFD$ behaves similar to case a.).

In case c.) we have a focused star. Then the distribution of flux changes so that more flux is in the center of the centroid. The $HFD$ decreases. Note that the $HFD$ even gives acceptable values for stars which are quite far out of focus. This makes it generally more stable than the FWHM method.

C++ Implementation

NOTE: All the source codes of this “Night sky image processing” series presented in part 1-7 are also available on github in the star_recognizer repository.

Below is the C++ code for my HFD implementation. The second part of the code just generates an image to demonstrate the effect of HFD for different star images. The test data is available here.

#include <iostream>
#include <assert.h>
#include <CImg.h>
#include <CCfits/CCfits>
 
using namespace std;
using namespace cimg_library;
using namespace CCfits;
 
void readFile(CImg<float> & inImg, const string & inFilename) {
  std::auto_ptr<FITS> pInfile(new FITS(inFilename, Read, true));
  PHDU & image = pInfile->pHDU(); 
  inImg.resize(image.axis(0) /*x*/, image.axis(1) /*y*/, 1 /*z*/, 1 /*1 color*/);
  
  // NOTE: At this point we assume that there is only 1 layer.
  std::valarray<unsigned long> imgData;
  image.read(imgData);
  cimg_forXY(inImg, x, y) { inImg(x, inImg.height() - y - 1) = imgData[inImg.offset(x, y)]; }
}
 
/**
 * Get all pixels inside a radius: https://stackoverflow.com/questions/14487322/get-all-pixel-array-inside-circle
 * Algorithm: https://en.wikipedia.org/wiki/Midpoint_circle_algorithm
 */
bool insideCircle(float inX /*pos of x*/, float inY /*pos of y*/, float inCenterX, float inCenterY, float inRadius) {
  return (pow(inX - inCenterX, 2.0) + pow(inY - inCenterY, 2.0) <= pow(inRadius, 2.0));
}
 
/**
 * Expects star centered in the middle of the image (in x and y) and mean background subtracted from image.
 *
 * HDF calculation: https://www005.upp.so-net.ne.jp/k_miyash/occ02/halffluxdiameter/halffluxdiameter_en.html
 *                  https://www.cyanogen.com/help/maximdl/Half-Flux.htm
 *
 * NOTE: Currently the accuracy is limited by the insideCircle function (-> sub-pixel accuracy).
 * NOTE: The HFD is estimated in case there is no flux (HFD ~ sqrt(2) * inOuterDiameter / 2).
 * NOTE: The outer diameter is usually a value which depends on the properties of the optical
 *       system and also on the seeing conditions. The HFD value calculated depends on this
 *       outer diameter value.
 */
float calcHfd(const CImg<float> & inImage, unsigned int inOuterDiameter) {
  // Sum up all pixel values in whole circle
  float outerRadius = inOuterDiameter / 2;
  float sum = 0, sumDist = 0;
  int centerX = ceil(inImage.width() / 2.0);
  int centerY = ceil(inImage.height() / 2.0);
 
  cimg_forXY(inImage, x, y) {
    if (insideCircle(x, y, centerX, centerY, outerRadius)) {
      sum += inImage(x, y);
      sumDist += inImage(x, y) * sqrt(pow((float) x - (float) centerX, 2.0f) + pow((float) y - (float) centerY, 2.0f));
    }
  }
  // NOTE: Multiplying with 2 is required since actually just the HFR is calculated above
  return (sum ? 2.0 * sumDist / sum : sqrt(2.0) * outerRadius);
}
 
 
int main( int argc, char *argv[]) {
  // For all filenames specified
  const size_t numCols = 4;
  const size_t numRows = ceil((float) argc / (float) numCols);
  const size_t imgWidth = 65, imgHeight = 85; // Hardcoded image size
  CImg<unsigned char> containerImg(numCols * imgWidth, numRows * imgHeight, 1/*depth*/, 3 /*3 channels - RGB*/);
 
  for (size_t i = 1; i < argc; ++i) {
    CImg<float> img;
  
    try {
      readFile(img, argv[i]);
    } catch (FitsException &) {
      cerr << "Read FITS failed." << endl;
      return 1;
    }
 
    // Subtract mean value from image which is required for HFD calculation
    CImg<float> img2(img);
    double mean = img.mean();
    
    cimg_forXY(img, x, y) {
      if (img(x, y) < mean) {
        img2(x, y) = 0;
      } else {
        img2(x, y) = img(x, y) - mean;
      }
    }
 
    // Calc the HFD
    const unsigned int outerDiameter = 60;
    float hfd = calcHfd(img2, outerDiameter /*outer diameter in px*/);
 
    cerr << "File " << argv[i] << " -> hfd: " << hfd << endl;
 
    
    // Create RGB image from fits file to paint circle (just for visualization)
    CImg<unsigned char> rgbImg(img2.width(), img2.height(), 1 /*depth*/, 3 /*3 channels - RGB*/);
    float min = img2.min(), mm = img2.max() - min;
    
    cimg_forXY(img2, x, y) {
      int value = 255.0 * (img2(x,y) - min) / mm;
      rgbImg(x, y, 0 /*red*/) = value;
      rgbImg(x, y, 1 /*green*/) = value;
      rgbImg(x, y, 2 /*blue*/) = value;
    }
    
    // Draw circles and text
    ostringstream oss;
    oss.precision(4);
    oss << "HFD" << endl << "~" << hfd;
    
    const unsigned char red[3] = { 255, 0, 0 }, green[3] = { 0, 255, 0 }, yellow[3] = { 255, 255, 0 }, black[3] = { 0, 0, 0 };
    rgbImg.draw_circle(img2.width() / 2, img2.height() / 2, outerDiameter / 2, red, 1 /*pattern*/, 1 /*opacity*/);
    rgbImg.draw_circle(img2.width() / 2, img2.height() / 2, hfd / 2, green, 1 /*pattern*/, 1 /*opacity*/);
    rgbImg.draw_text(0 /*x0*/, 0 /*y0*/, oss.str().c_str(), yellow /*fg color*/, black /*bg color*/, 0.7 /*opacity*/, 14 /*font-size*/);
 
    // Add rgb image to "container" image
    size_t rowIdx = floor((float)(i - 1) / 4.0f);
    size_t colIdx = (i - 1) % 4;
    containerImg.draw_image(imgWidth * colIdx, imgHeight * rowIdx, rgbImg);
  }
 
  // Display the container image
  CImgDisplay imgDisp(containerImg, "Image");
  while (! imgDisp.is_closed()) {
    imgDisp.wait();
  }
  
  return 0;
}

The source file can also be downloaded here. The command to compile the code above is:

g++ hfd_calc.cpp -o hfd_calc -lCCfits -lcfitsio -lX11 -lpthread

The result

The output when executing is:

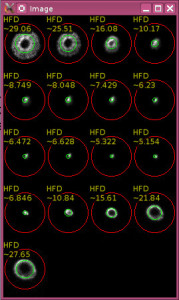
./hfd_calc focus_test/focus_test_570.fit focus_test/focus_test_577.fit focus_test/focus_test_587.fit
focus_test/focus_test_594.fit focus_test/focus_test_595.fit focus_test/focus_test_596.fit
focus_test/focus_test_597.fit focus_test/focus_test_598.fit focus_test/focus_test_599.fit
focus_test/focus_test_600.fit focus_test/focus_test_601.fit focus_test/focus_test_602.fit
focus_test/focus_test_607.fit focus_test/focus_test_611.fit focus_test/focus_test_617.fit
focus_test/focus_test_624.fit focus_test/focus_test_630.fit
File focus_test/focus_test_570.fit -> hfd: 29.0583
File focus_test/focus_test_577.fit -> hfd: 25.5133
File focus_test/focus_test_587.fit -> hfd: 16.0802
File focus_test/focus_test_594.fit -> hfd: 10.1732
File focus_test/focus_test_595.fit -> hfd: 8.74913
File focus_test/focus_test_596.fit -> hfd: 8.04788
File focus_test/focus_test_597.fit -> hfd: 7.42914
File focus_test/focus_test_598.fit -> hfd: 6.23011
File focus_test/focus_test_599.fit -> hfd: 6.472
File focus_test/focus_test_600.fit -> hfd: 6.6277
File focus_test/focus_test_601.fit -> hfd: 5.32163
File focus_test/focus_test_602.fit -> hfd: 5.15386
File focus_test/focus_test_607.fit -> hfd: 6.84554
File focus_test/focus_test_611.fit -> hfd: 10.8415
File focus_test/focus_test_617.fit -> hfd: 15.6092
File focus_test/focus_test_624.fit -> hfd: 21.8362
File focus_test/focus_test_630.fit -> hfd: 27.6515

Note that the test images have been centred manually. Hence the accuracy

might not be the best. Still, there are two conclusions which can be drawn from the right image:

• The green circle ($HFD$) correlates very well with the star focus
• It even correlates when the star is far out of focus

In the final part – Part 7 of my “Night sky image processing” Series I will put all the things together.

Last updated: June 9, 2022 at 23:44 pm